700 tysięcy dolarów za rozwikłanie matematycznej zagadki
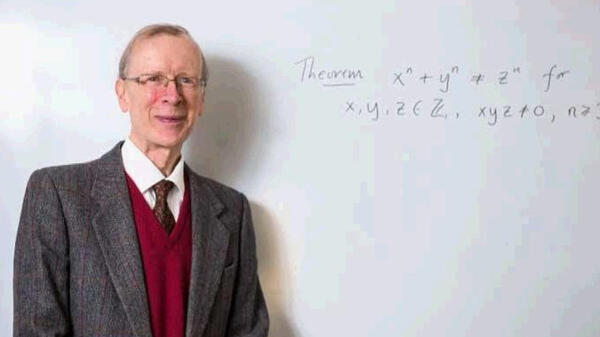
To był problem, który "nękał" matematyków przez stulecia. Za rozwiązanie równania z 1637 roku, autorstwa matematyka Pierre de Fermata, brytyjski profesor z uniwersytetu w Oksfordzie Andrew J. Wiles otrzymał 700 tysięcy dolarów oraz prestiżową nagrodę Abela.
Andrew J. Wiles na rozwiązanie równania poświęcił 50 lat życia. Swój dowód brytyjski matematyk przedstawił w 1993 roku, a teraz otrzymał za niego od króla Norwegii prestiżową nagrodę w dziedzinie matematyki oraz 700 tysięcy dolarów.
Otrzymując nagrodę, naukowiec podkreślił, że jest to dla niego wielki zaszczyt, gdyż równanie fascynowało go od dzieciństwa. – Poznałem równanie, gdy miałem 10 lat. Wiedziałem, że muszę je rozwiązać – mówił matematyk, komentując swój sukces.
Równanie powstało w 1637 roku, rozpisał je matematyk Pierre de Fermat i od tego czasu spędzało ono sen z powiek matematykom na całym świecie. Słynne "Wielkiego Twierdzenia Fermata" mówi, że „dla liczby naturalnej n>2 nie istnieją takie liczby naturalne dodatnie x,y,z, które spełniałyby równanie x^n+y^n=z^n”. Dowód na to twierdzenie przeprowadził dopiero brytyjski naukowiec ponad 350 lat później.
NAS member and NAS Award in Math recipient Andrew Wiles solved 300-year-old math equation: https://t.co/vA7K4F8ShA pic.twitter.com/7GcSMFu8Sg
— NatlAcad of Sciences (@theNASciences) 17 marca 2016
Polecamy Hity w sieci
Wiadomości
Szczucki: koalicja Tuska jest przerażona,ich projekt oddania władzy Tuskowi nie może być realizowany
Ogólnokrajowa konferencja „Forum Pracownika i Pracodawcy” już za nami. Przed nami czas na poznanie jej dorobku
Morawiecki: rząd nie kontroluje polskich granic, codziennie okłamują Polaków, musimy to zatrzymać [WIDEO]
Kluby "Gazety Polskiej" pod budynkiem Sądu Najwyższego. Bąkiewicz: apeluję do Was, przybądźcie na protest [WIDEO]
Nawrocki z pierwszą wizytą prezydencką uda się do USA? Szefernaker: to nasze kampanijne zobowiązanie
Najnowsze
Szczucki: koalicja Tuska jest przerażona,ich projekt oddania władzy Tuskowi nie może być realizowany
Morawiecki: rząd nie kontroluje polskich granic, codziennie okłamują Polaków, musimy to zatrzymać [WIDEO]
Kluby "GP" pod budynkiem SN. Sakiewicz: jesteśmy krajem, w którym gwałci się wolność słowa
Patrioci bronią Sądu Najwyższego. Dochodzi do prowokacji, policja znów zawodzi [TRANSMISJA]
